I always loved doing programming puzzles and algorithms were always my favourite part of any Computer Science course. I remembered this once again when I stumbled across Day 6 of 2015 Advent of Code. I was doing those puzzles as I was yearning for logical puzzles and also wanted to get more familiar with Go programming language, which is getting more and more popular for writing high performance backend services.
Puzzle
Idea of the puzzle is very simple. You are given set of instructions that turn on, turn off or toggle subset of lights in the grid. You should execute those instructions and count how many lights are lit after executing all instructions.
We can define every instruction as the following:
(x1,y1) -> (x2,y2) [action]
Where x1 and y1 mark leftmost corner and x2 and y2 mark the rightmost corner of the rectangle.
Approach
First I looked at the size of the grid (1000 x 1000) and saw that we have at most 1.000.000 lights. Then I looked at the number of instruction in the puzzle input and saw that there are 300 instructions. I correctly deduced that numbers in this puzzle are small enough that we can solve this task just by doing what puzzle instructions say.
Basic algorithm
I parsed the input to get instructions in suitable format and then initialized empty map that represented my grid. Key represented location (x,y) on the grid and value was boolean value that indicated whether light on that location was lit.
Then I started iterating through instructions. For every instruction, I had to iterate through every light in the instruction’s area and set value in map to true or false based on current light state (on or off) that I read from the map and instruction’s action (turn on, turn off or toggle). After doing this for every instruction I then only needed to iterate through all the keys on the map and count number of keys whose values were true (= light was lit).
Algorithm is very simple so there were no problems with writing that code. I ran it, waited a bit to get the result and correctly solved the puzzle. Second part of the puzzle is trivial as we only need to calculate brightness instead of whether lights are on or off based on set of rules.
Sweeping algorithm
But before I started solving the problem with that straightforward approach I already knew, that this is a dummy way to do it. Morover, this approach only works because grid and the number of instructions is small. If instructions’ areas were larger then algorithm would work very slowly.
Therefore I decided to try to solve this problem with better approach that would work no matter how large the grid or the rectangles are. I decided to name this algorithm as a Sweeping Algorithm because it resembles the family of Sweeping line algorithms that use sweeping line to solve problems in computational geometry. One example of that is the Fortune’s algorithm for generating Voronoi diagrams from the set of points in the plane.
How to count the lights?
The main drawback of the basic algorithm is that it is iterating through every light of the instruction’s rectangle. In ideal world we would like to only calculate the area of the rectangles and apply action on that area as whole. But this is not an ideal world as rectangles can overlap and not only that - the order in which they overlap is important too. There is a difference if we first turn the light off and then turn it on or if we do that in reverse.
Let’s introduce Example 1:
(1,1) -> (4,4) [turn on]
(2,2) -> (3,3) [turn off]
(3,3) -> (5,5) [turn on]
On Figure 1 we can see visualization of the Example 1:
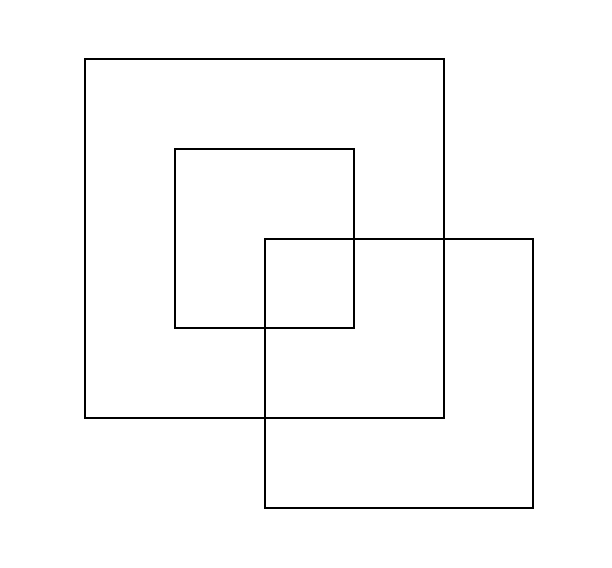
I thought about this and figured out that we could just find all complete overlaps and non-overlaps and find which instructions are controlling those areas. As I wanted to compute areas of complete overlaps easily I stuck to rectangles. Therefore we only need to split all rectangles to smaller rectangles that do not overlap or overlap completely and are part of the same set of instructions.
One of the possible splits for Example 1 is seen on Figure 2:
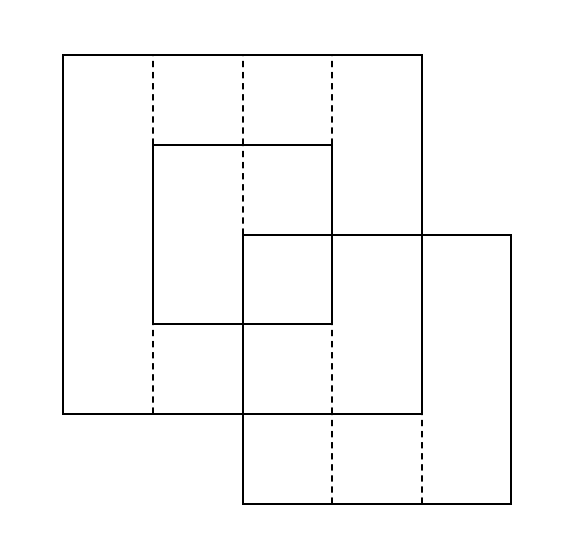
Instead of 3 rectangles that are partially overlapping we now have 13 rectangles that are not overlapping or are overlapping completely. For every such rectangle we first sort the instructions by order in which they appeared in the input and then compute only one scalar: 1 if sequence of instructions causes lights on or 0 if lights are off. Then we multiply this scalar by area of the rectangle, sum values over all rectangles and get the result.
If we do this by hand for Example 1 we get the following:
(1,1) -> (1,4) [turn on]: 4
(2,1) -> (2,1) [turn on]: 1
(2,2) -> (2,3) [turn on, turn off]: 0
(2,4) -> (2,4) [turn on]: 2
(3,1) -> (3,1) [turn on]: 1
(3,2) -> (3,2) [turn on, turn off]: 0
(3,3) -> (3,3) [turn on, turn off, turn on]: 0
(3,4) -> (3,4) [turn on, turn on]: 1
(3,5) -> (3,5) [turn on]: 1
(4,1) -> (4,2) [turn on]: 2
(4,3) -> (4,4) [turn on, turn on]: 2
(4,5) -> (4,5) [turn on]: 1
(5,3) -> (5,5) [turn on]: 3
-----------------------------------------------
Sum: 18
How to compute the rectangles?
The “hard” part of this problem is not the counting of lights turned on when we already have the rectangles, but how to efficiently split those instructions into smaller non-overlapping rectangles.
This is where sweeping comes into play!
In order to calculate those rectangles efficiently we should jump over lights and not move over them one by one.
Let’s imagine that we have sweepLineX which only goes through vertical rectangle edges. And we also have sweepLineY that will go through horizontal edges that are present between current sweepLineX and the next one. If we check Example 1, the values for sweepLineY when sweepLineX = 2 are [1, 2, 4, 5]. And consecutive values of sweepLineY represent borders of rectangle (values are inclusive). For those values we therefore produce the following rectangles:
(2,1) -> (2,1)
(2,2) -> (2,3)
(2,4) -> (2,4)
While we are sweeping across our instructions we should also keep record of instructions that are currently active in x and y directions. Instruction (x1,y1) -> (x2,y2) is active for sweepLineX and sweepLineY if:
x1 <= sweepLineX && x2 > sweepLineXy1 <= sweepLineY && y2 > sweepLineY
Note: it depends on how you represent and handle coordinates, those conditions can vary if you are handling coordinates as inclusive or as exclusive.
This is the main idea of the whole approach. It is a bit more complicated than the basic approach, because the problem is visual and therefore easier to understand. But as it often happens:
Visual programming puzzles are easy to understand but hard to code.
Some carefulness is needed, you can see my implementation in Go here: link.
Analysis
But why would we bother with implementation of sweeping algorithm if basic approach works? The answer is that it works for this size of the problem, but as soon as we increase the sizes of rectangles by larger factors we see the real difference in execution time:
| Factor | Basic Algorithm | Sweeping Algorithm |
|---|---|---|
| 1 | 3.2 s | 950 ms |
| 2 | 13 s | 950 ms |
| 5 | 1 m 33s | 950 ms |
| 10 | 7 m 22s | 950 ms |
| 100 | / | 950 ms |
| 1000 | / | 950 ms |
As we can see from the Table 1, the difference in execution is significant. For sweeping algorithm, the execution time stays the same while it increases a lot for basic algorithm. It increases to an extent that the algorithm becomes useless for larger rectangles. Moreover, sweeping algorithm could be further optimized with usage of better data structures and optimizations of some iterations.
Conclusion
The size of the problem greatly influences the choice of the approach we need to take. If the problem is relatively small (as it was orignally in the Advent of Code puzzle) we can get away with the simple and straightforward solution. But if we up the ante and try a bit harder, we can come up with beautiful and very efficient algorithms which are worth the effort.